Warren’s long burgers math

publish Opened 2025-01-11.

Context

This article shows how I made the OpenSCAD diagram in Warren’s long burgers. I wanted to visualize my belief that widening a burger while using the same amount of ingredients produces a way more appealing sandwich.

The math

We’ll first represent a 65 unit tall burger as a cylinder:

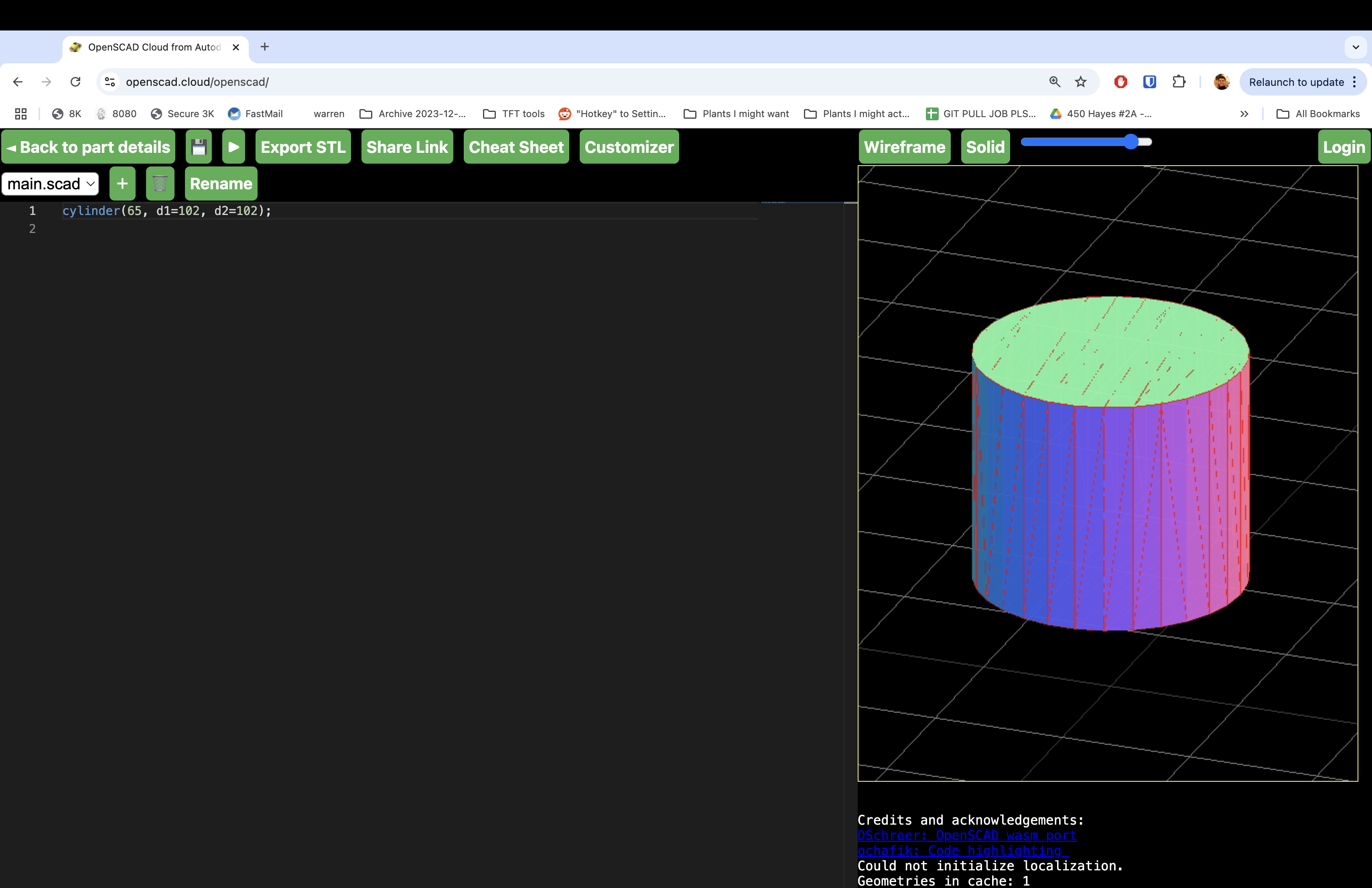Cylinder of height 65, radius 51

We’re using 65 units because an NIH study in 2016 estimated an average adult’s maximum mouth opening as 52 +/- 5mm. So a 65 unit tall burger is too tall — but if we adjust its height to something more reasonable, say 47mm, while keeping volume constant, we can visualize what a physically edible version of the same sandwich looks like.

Math time

We calculate a cylinder’s volume like so: $$volume_{before} = h \pi r^2$$

Plugging in our known values: $$volume_{before} = 65*\pi*51^2 ≈ 531,133$$

Which we can adjust for a new height of 47, like so:

$$47*\pi*r_{new}^2 = 531,133$$

Rearranging to solve for $r_{new}$:

$$r_{new} = \sqrt{\frac{531,133}{47*\pi}} ≈ 59.98$$

So, our new radius is roughly 60 (assuming a cylindric burger).

… and that’s it. Pretty simple math!

But let’s do it on a per-ingredient basis

Let’s start with the ingredient ratios for the Platonic unideal of a 65mm tall burger (which we will double to 130 units to avoid decimals.

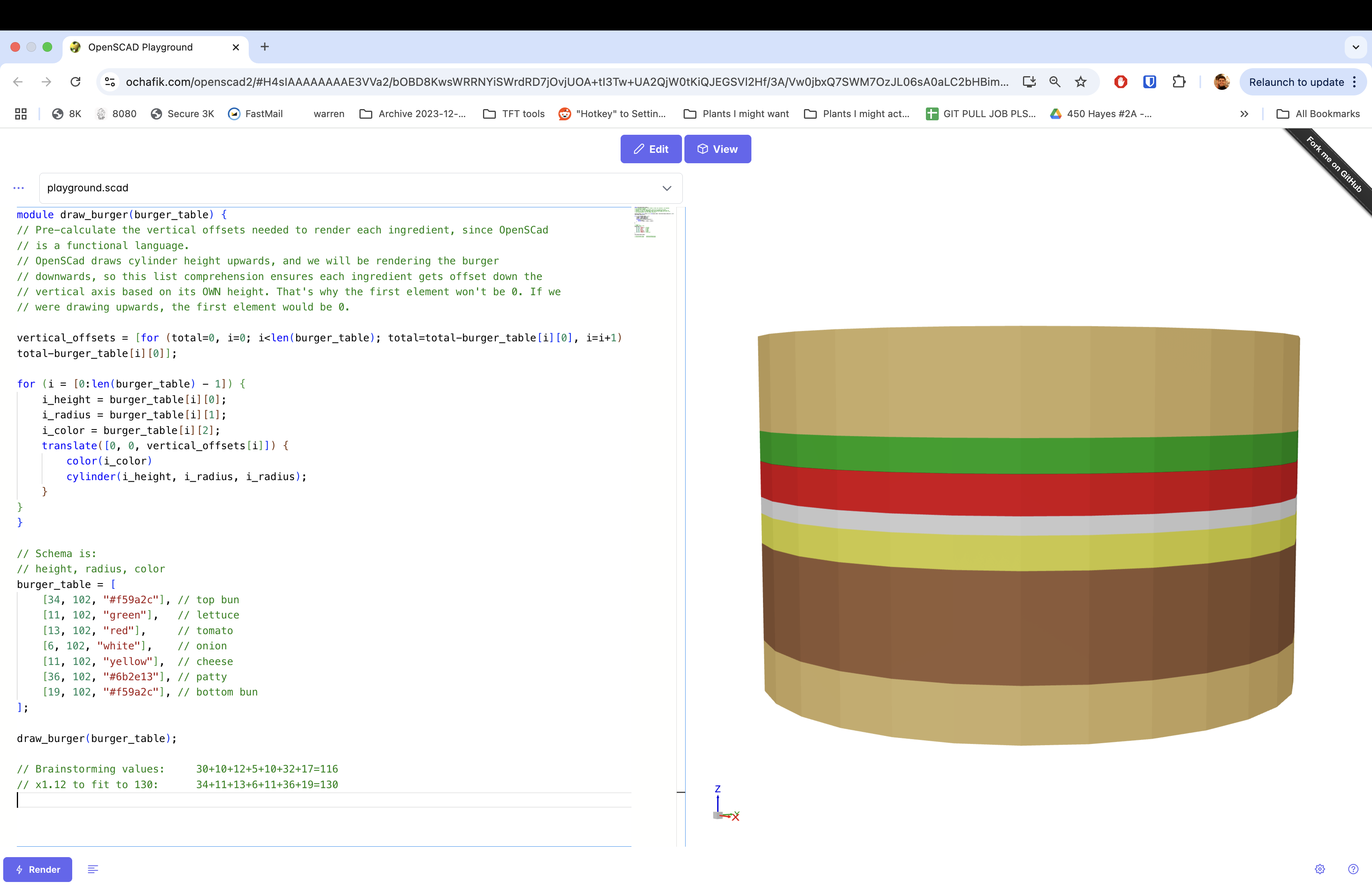Bask in its mediocre radiance

We want to squash this burger from 65*2=130 units to 47*2=94 units. We already know the radius that we want all the ingredients to have from the math above: 59.98

So we can just plug that in like so:

$$h r^2 = h_{new} r_{new}^2$$

$$h_{new} = \frac{h r^2}{r_{new}^2}$$

$$h_{new} = \frac{h * 51^2}{59.98^2} ≈ \frac{h * 2601}{3597.6}$$

Yielding our table:

Ingredient	Height before	Height after	Height after rounding
Top bun	34	24.581	25
Lettuce	11	7.953	8
Tomato	13	9.388	9
Onion	6	4.338	4
Cheese	11	7.953	8
Patty	36	26.027	26
Bottom bun	19	13.737	14
Total	130	93.988	94

Radius before	Radius after
51	~60

The visualization:

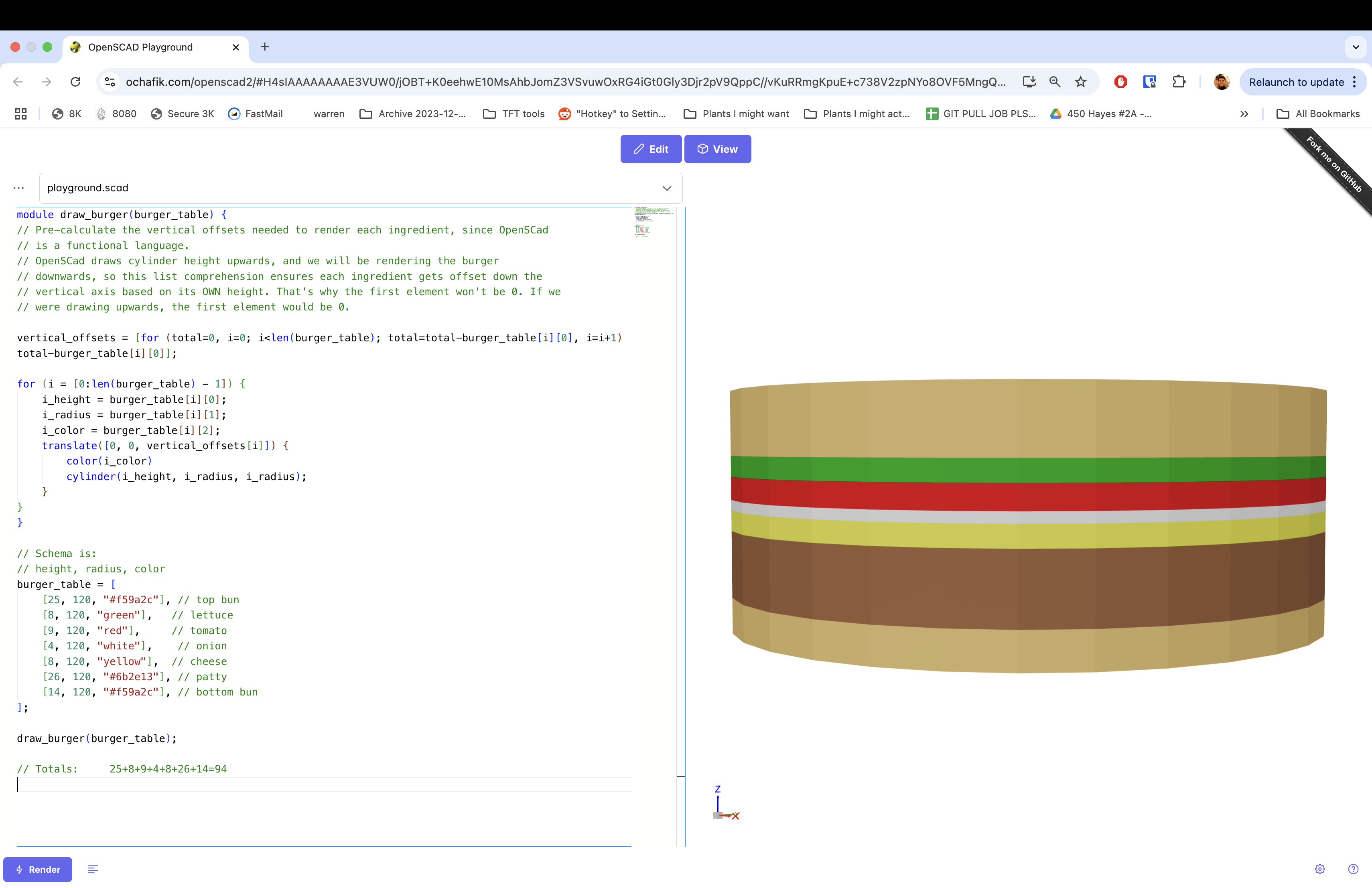Bask in its reasonableness

It’s the same volume!!

Closing notes

On squish factor

You may have missed how surprisingly small the units above are:

65mm = 2.56in (our original, “too tall” burger)
47mm = 1.85in (our new “reasonable” burger)

2.56 inches is roughly the height of an McDonald’s Big Mac in America and they are pretty edible, so something’s missing from our calculation.

I think what’s missing is squish factor. When you compress a burger with your hands, it loses some height, making tall burgers into reasonable size.

If we extrapolate based on the Big Mac behavior — that a 65mm tall burger may squish down to an edible height of ~47mm at consumption time — we can make the following assumptions:

A 65mm tall burger compresses down to 47mm (~72.5% of its original size).
The bun probably compresses more than the rest of the ingredients.

Using some intuition/imagination, we can guesstimate:

A Big Mac bun compresses ~50% (26.5 ⇒ 13.25).
The ingredients of a Big Mac compress ~13% (38.5 ⇒ 33.75).
Total is 47.

(Granted this is a pretty generous assessment of a Big Mac. Big Macs have a third bun in their center, so the real squish factor will be lower in order to account for more bun.)

Anyways. What this means is that a burger may in fact be edible despite being >47mm tall. If you think your burger is similar to a Big Mac in ingredients/texture, you just need to multiply your bun height by 0.5 and your ingredient height by 0.87. If the resulting height is ⇐47mm, your burger is edible at consumption time; else, you’ll need to flatten it out more.

On the cost of Long Burgers

Flattening burger ingredients is trivial (you just squish them when cooking the burger). Flattening burger buns isn’t, because you’re stuck with whatever size you bought from the store. If you’re a low to mid-scale restaurant using store-bought buns, we’re cool. No need to suffer my pedantry; use whichever size bun you happen to have on you.

HOWEVER if you’re a restaurant I dined at on The best burger in the bay area charging >$20 a burger, there are quality standards to clear. Why not use flatter buns? There’s virtually no monetary cost involved. If you’re baking your own buns in house, just reshape the dough. Use a measuring tape if you need. Fancy restaurants often have those anyways.

OK thanks for reading.

Appendix

My OpenSCAD code:

module draw_burger(burger_table) {
// Pre-calculate the vertical offsets needed to render each ingredient, since OpenSCad
// is a functional language.
// OpenSCad draws cylinder height upwards, and we will be rendering the burger
// downwards, so this list comprehension ensures each ingredient gets offset down the
// vertical axis based on its OWN height. That's why the first element won't be 0. If we
// were drawing upwards, the first element would be 0.

vertical_offsets = [for (total=0, i=0; i<len(burger_table); total=total-burger_table[i][0], i=i+1) total-burger_table[i][0]];

for (i = [0:len(burger_table) - 1]) {
    i_height = burger_table[i][0];
    i_radius = burger_table[i][1];
    i_color = burger_table[i][2];
    translate([0, 0, vertical_offsets[i]]) {
        color(i_color)
        cylinder(i_height, i_radius, i_radius);
    }
}
}

// Schema is:
// height, radius, color
burger_table = [
    [34, 102, "#f59a2c"], // top bun
    [11, 102, "green"],   // lettuce
    [13, 102, "red"],     // tomato
    [6, 102, "white"],    // onion
    [11, 102, "yellow"],  // cheese
    [36, 102, "#6b2e13"], // patty
    [19, 102, "#f59a2c"], // bottom bun
];

draw_burger(burger_table);

// Brainstorming values:     30+10+12+5+10+32+17=116
// x1.12 to fit to 130:      34+11+13+6+11+36+19=130

OpenSCAD online tools I used:

Perdicis Notes

Explorer